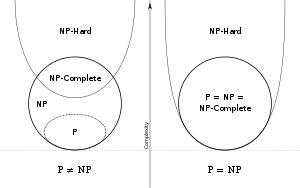
P: problems quickly solvable

NP: problems quickly checkable

Quick means the existence of an algorithm solving the task that runs in polynomial time.

If it turned out that P ≠ NP, which is widely believed, it would mean that there are problems in NP that are harder to compute than to verify.

Many of the problems in NP have the extra property that a fast solution to any one of them could be used to build a quick solution to any other problem in NP, a property called NP-completeness. An NP-complete problem is an NP problem that is at least as "tough" as any other problem in NP.

NP-hard problems are those at least as hard as NP problems.