https://www.nature.com/articles/nbt1406
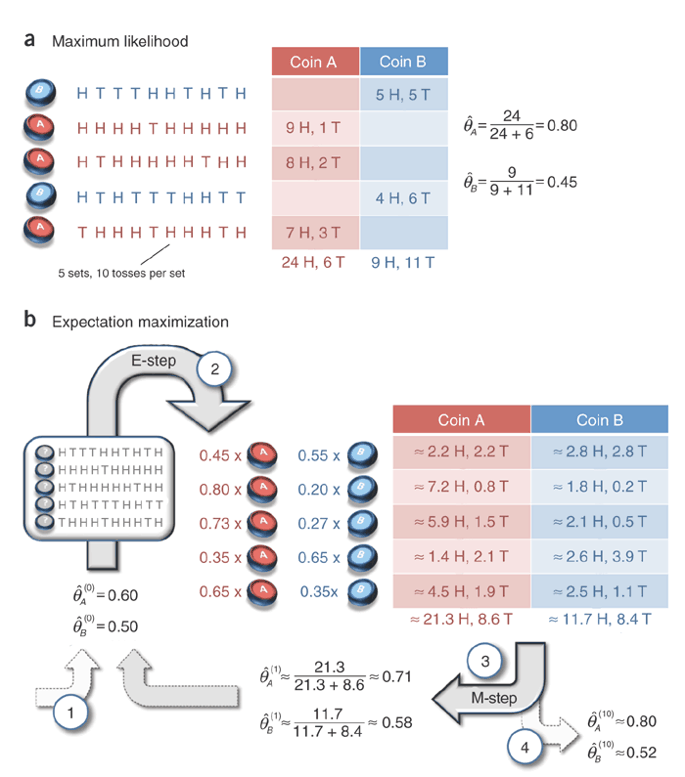
We want to estimate the probability of coin A and B handing on head: theta_A, theta_B, with 5 observations of number of heads among 10 flips x_i {1,2,..10} with record of which coin is flipping z_i {A,B}
If both x and z are available, we can calculate the total number of heads for A =24, divided by total flip number = 30, so the maximum likelihood of theta_A = 24/30=0.8, theta_B = 9/20 = 0.45.
But if z is not available, we can use Estimation-Maximum to 1) guess probability of flipping coin A/B, then 2) estimate likelihood of head for A/B. Iterate step 1 and 2 until converge to estimate theta_A/B.
For example, initial guess can be theta_0_A=0.6, theta_0_B=0.5. Coin flipping follows Binomial distribution, the probability function is P(n,k,theta) = C(n,k)*theta^k*(1-theta)^k. For first 10 flips, for example, n=10, k=5, the probability of flipping coin A is C(10,5)*0.6^5*0.4^5=0.2006581248, for B is C(10,5)*0.5^5*0.5^5=0.24609375, the normalized portion for A is (0.200/0.200+0.246)=0.448, B is 0.552. So the flip counts are divided as if flipping 0.45 share of coin A and 0.55 share of coin B,5H5T becomes 2.2H2.2T for A and 2.8H2.8T for B. Similarly, for the second 10 flips, n=10, k=9, guessing portion of flipping A is C(10,9)*0.6^9*0.4 = 0.040310784, B is C(10,9)*0.5^9*0.5 = 0.009765625. Normalized to be 0.0403/(0.0403+0.0098)=0.804, and 0.196.
Aggregate all H and T for guessed coin flips for A and B, estimate new theta by total head portions. Until theta does not change, finally is 0.8 and 0.52.