When using BAFET to analyze brain vessels, I manually add tags to each image set based on subjective feeling. One of these tags are "Complete", meaning the completeness of cirlce of Willis exists in such case. Tag group meaning can be found in: http://clatfd.cn/a/212. 

The concern is whether a complete circle of Willis means richness of vessels?

To make contrast, compare cases marked as "Complete" with "Many" and "Few".  

The average total vessel length of "Complete" group is  3517.775, which is in the middle of "Few"(2098.074) and "Many"(4442.028) group, but closer to "Many". But they are only a little higer than the average of all cases (3421.427). In addition, the range of length in "Complete" group is wide. The smallest case is smaller than several cases marked as "Few", and the largest case is larger than most cases marked as "Many".

"Order 6+" vessel length is a number reflecting branch end richness. In cases tagged as "Complete", average total length of "Order 6+" vessels is 1850.775923, still between "Few" group (459.536) and "Many" group (3082.164), but a little higher than the average of all cases (1749.093).

A complete structure of vessel is broken when analyzing in order to be treated fairly with those without complete structure. Two more connected main arteries will largely increase length of vessel. So "Complete" group is comparable with other groups.

Based on these results above, I find in a brain with few vessels a complete circle of Willis is not easily found, but a complete circle of Willis is not a guarantee for more brain vessels. Fig 3.  show three cases with complete circle of Willis but different richness of vessels.

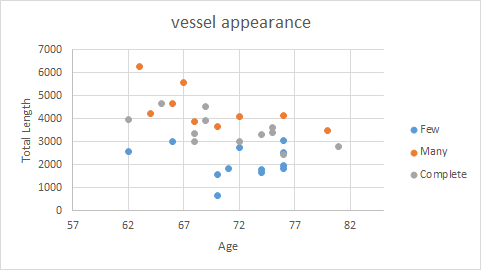
Fig 1. Total vessel length of brain between the group tagged as "Few", "Many" and "Complete"

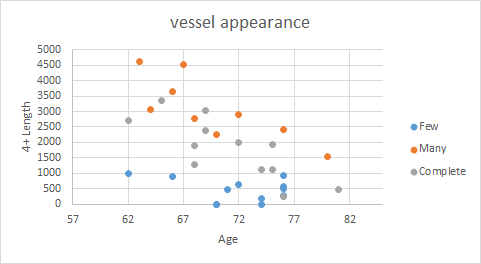
Fig 2. Order 6+ vessel length of brain between the group tagged as "Few", "Many" and "Complete"

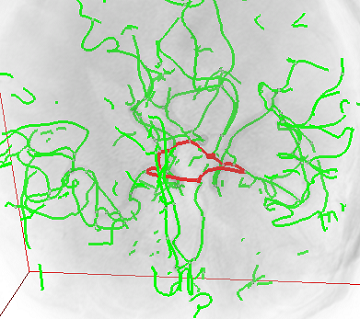
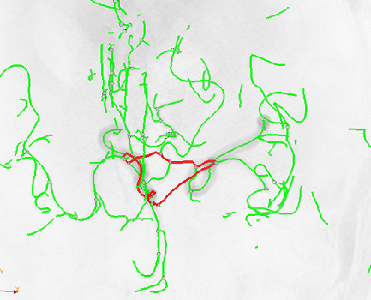
Fig 3. Samples of a complete circle of Willis (Total length: 4528.91, 3010.24, 2457.77)